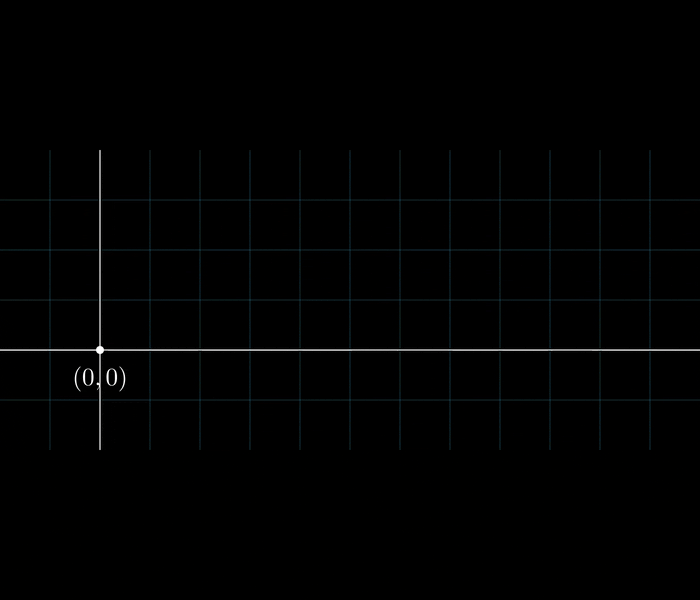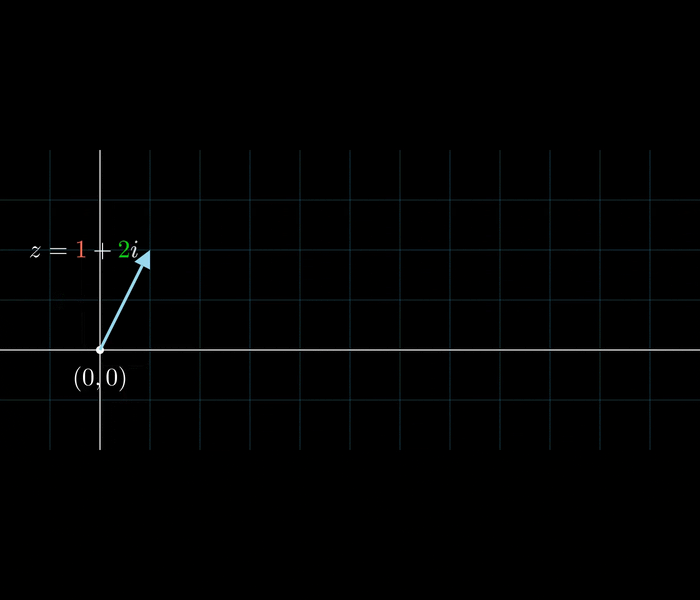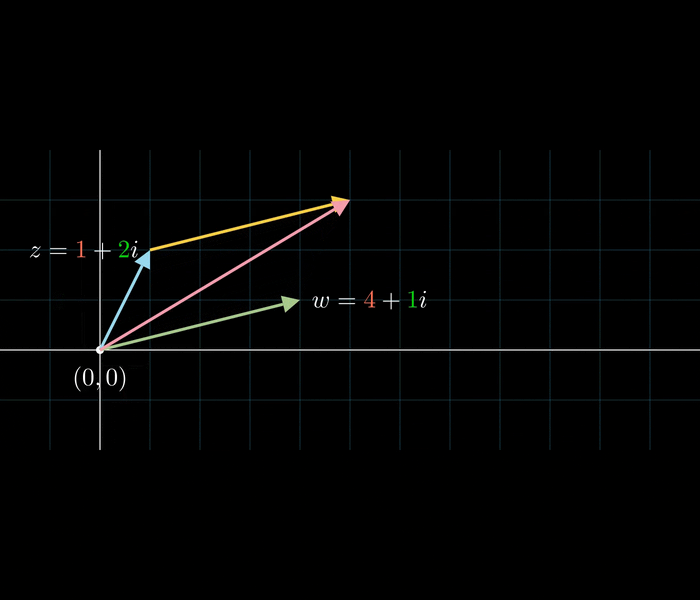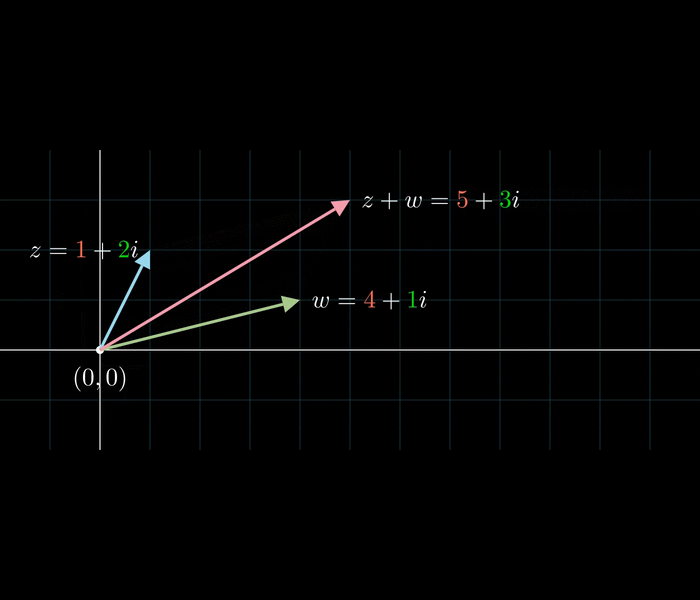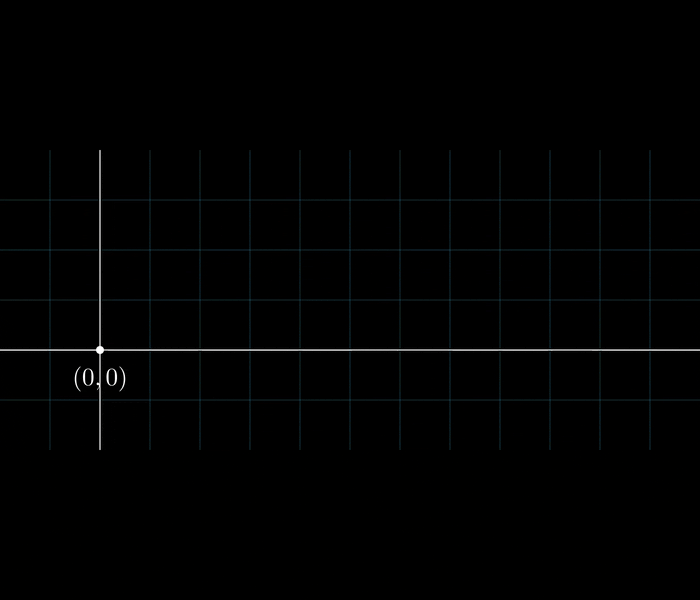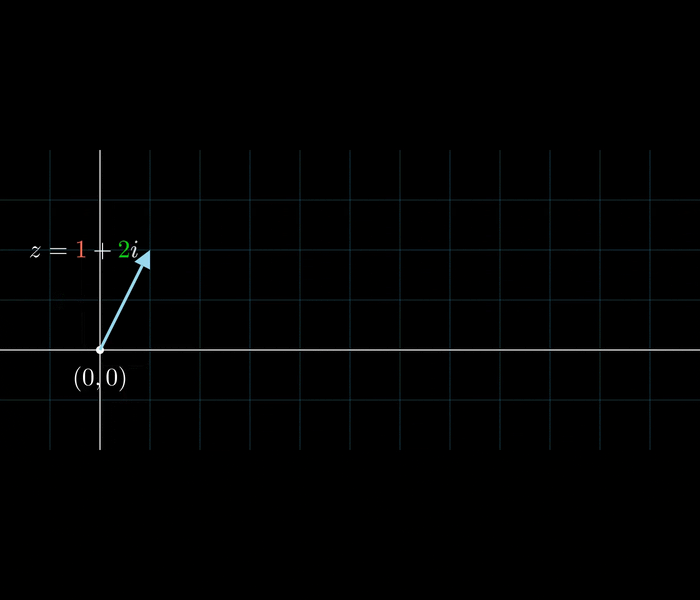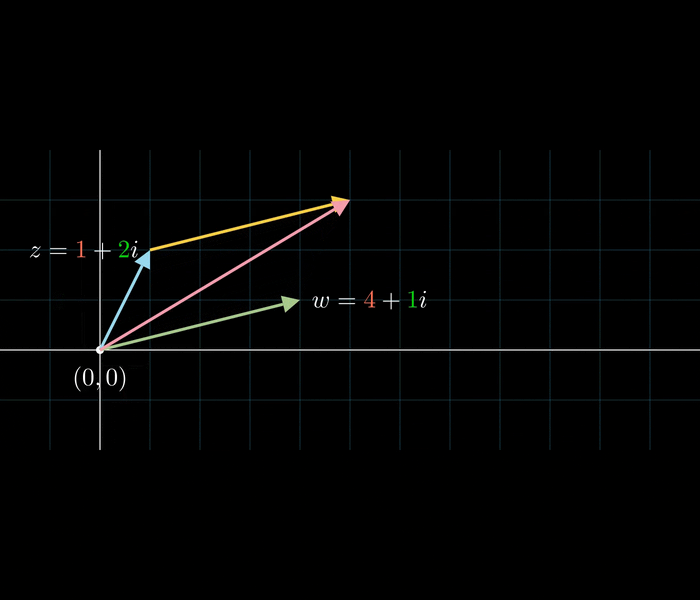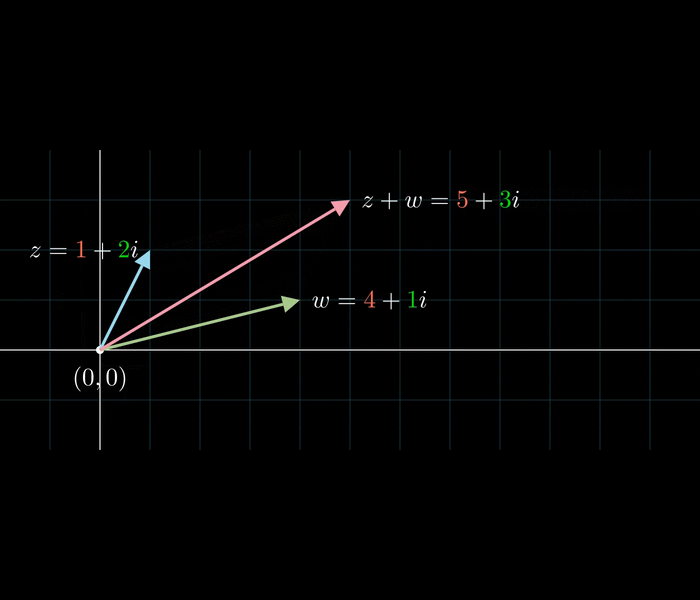Tutorium 0

Zurück zur Startseite

Kurzprotokoll

Wir haben mit Aufgabe 1 begonnen, wo wir neben den prinzipiellen Rechenregeln für Addition und komplexer Konjugation für Aufgabe (i) die folgenden Geogebra Applets für etwas geometrische Intuition besprachen:

1. |z + 1| = |z + 3|
2. 1/z = z̅
3. |z| = Re(z)+1

Daraufhin haben wir mithilfe der folgenden Animationen (auch hier als Videos verfügbar) geometrische Interpretationen der komplexen Addition und Multiplikation wiederholt:

Komplexe Addition

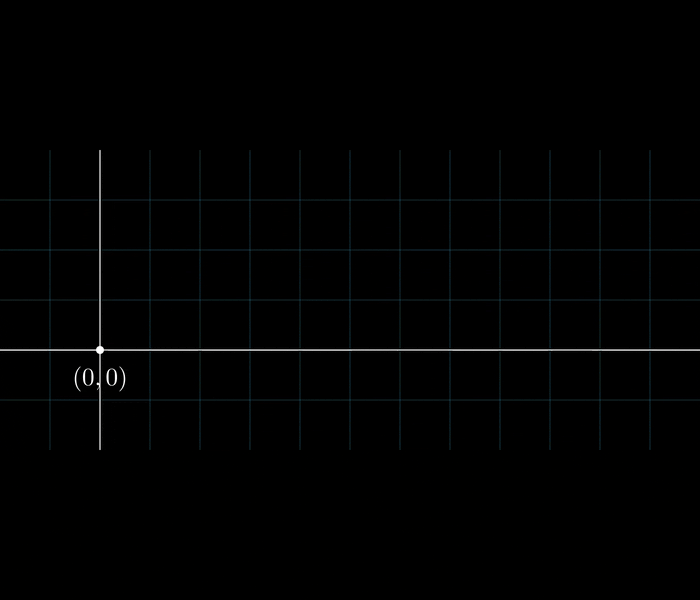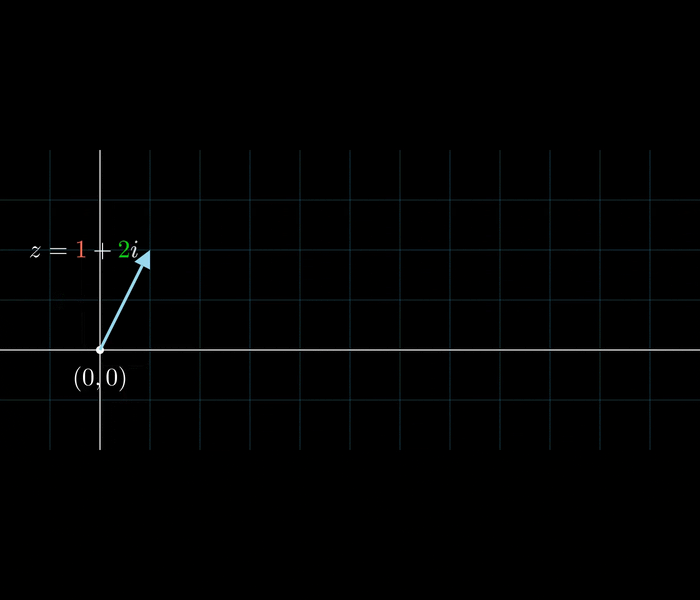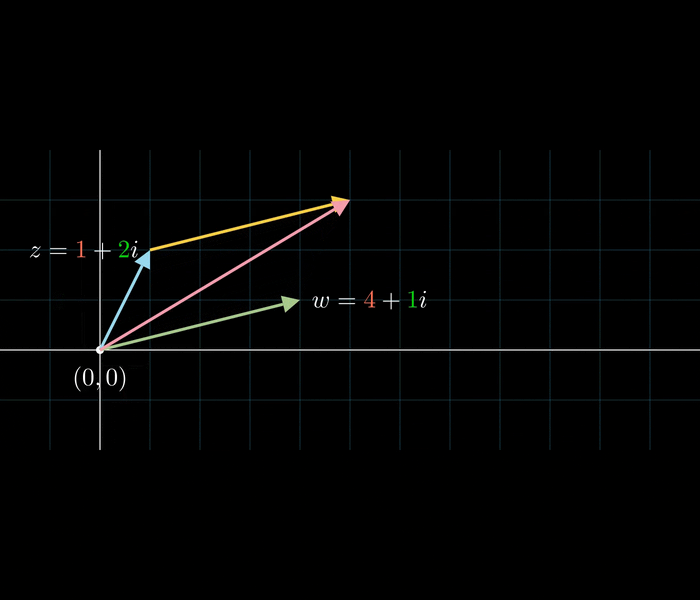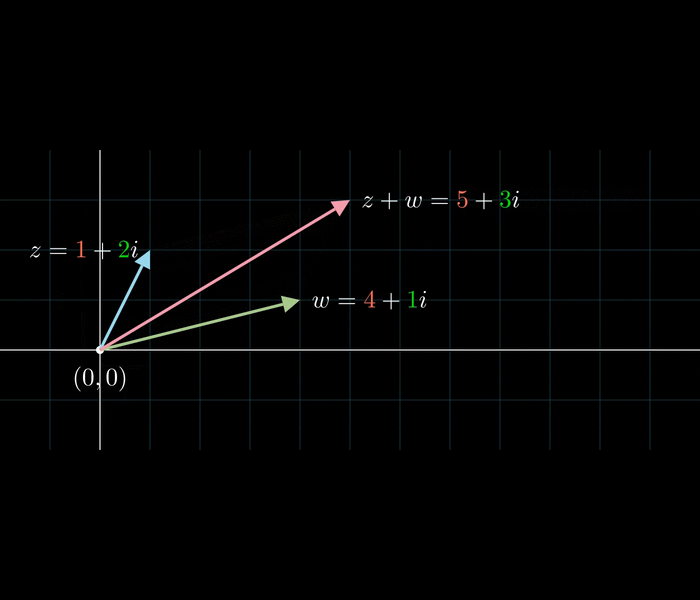
Komplexe Multiplikation

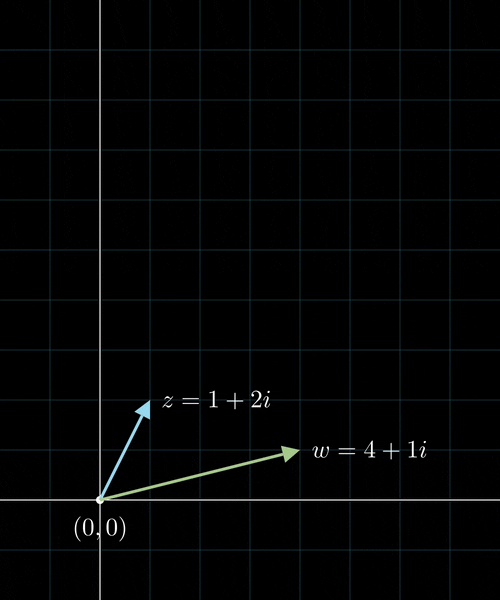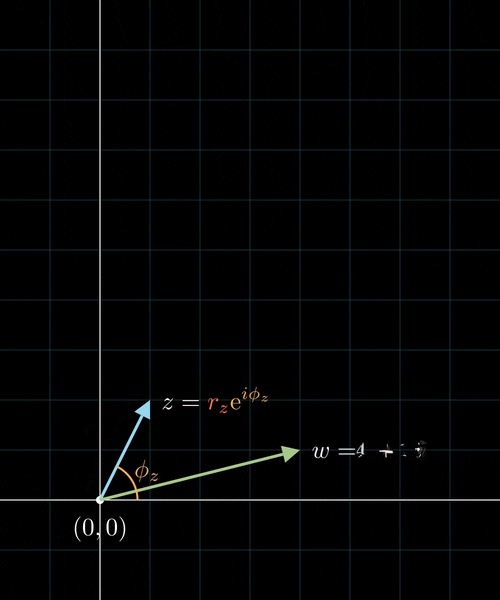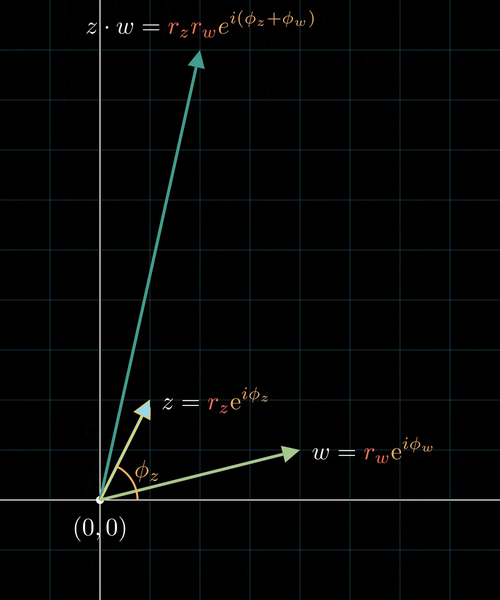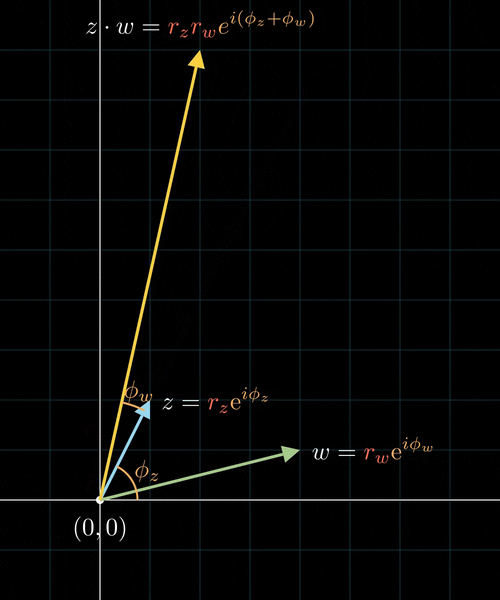
Komplexe Multiplikation als Rotation

Hieraufhin haben wir bei (iii) kurz über das Standardskalarprodukt auf \(\mathbb{C}\) geredet und mithilfe der (teils bekannten) Standardbeweisstrategie der Parallelogramm-Gleichung die Aufgabe gelöst.

Danach haben wir über die übrigen Aufgaben geredet.

Zum Mitnehmen

Aufgabe 1

• Komplexe Zahlen können viele geometrische Konstruktionen beschreiben, beispielsweise Kreise, Mittelsenkrechten, Inversion am (Einheits-)kreis, Spiegelung an Achsen oder Parabeln.
• Komplexe Multiplikation mit \(r e^{i \varphi}\) entspricht Skalierung um den Faktor \(r\) und Rotation um den Winkel \(\varphi\).
• “Faustregel”: Addition klappt besser mit kartesischen Koordinaten, Multiplikation klappt besser mit Polarkoordinaten.
• Rechenregeln für komplexes Konjugieren.
• Ist \(\lvert z \rvert = 1\) gegeben, so kann es hilfreich sein, \(z = e^{i \varphi}\) für \(\varphi \in [0, 2\pi)\) zu schreiben.

Aufgabe 2

• Geometrische Reihe (Konvergenzverhalten & Grenzwert).
• Konvergenzverhalten in Abhängigkeit des Konvergenzradius (und Definition des Letzteren).
• Cauchy-Hadamard und “Quotientenformel” (à la d’Alembert/Cauchy) zur Berechnung des Konvergenzradius.
• Potenzreihen können innerhalb des Konvergenkreises termweise differenziert werden und der Konvergenzradius ändert sich hierdurch nicht.

Aufgabe 3

• Definition partieller Ableitung und totaler Ableitung.
• Form der totalen Ableitung in Abhängigkeit der partiellen Ableitungen (Spalten der Jakobimatrix sind partielle Ableitungen).
• Um Nicht-Differenzierbarkeit zu zeigen, kann oft ein Widerspruchsbeweis hilfreich sein.
• Stetig differenzierbar \(\iff\) stetig partiell differenzierbar.

Fun Facts

Die Frage nach der Konvergenz einer Potenzreihe auf dem Rand des Konvergenzkreises (\(\lvert z \rvert = R\)) kann relativ weit geführt werden. Beispielsweise kann man sich überlegen, welche Teilmengen resultieren können, wenn diese genau die Punkte, für welche die Potenzreihe nicht konvergiert, beinhalten. \(\sum_{k=1}^{\infty} \frac{z^k}{k}\) konvergiert für alle \(\lvert z \rvert = 1\) mit \(z \neq 1\) und divergiert für \(z = 1\). Mittels Multiplikation von \(e^{\mathrm{i} \varphi}\) und Addition findet man nun recht schnell, dass jede endliche Teilmenge von \(\partial B_1(0)\) als “Nichtkonvergenzbereich” möglich ist.

Für eine deutlich ausführlichere Diskussion solcher Resultate mit Referenzen kann man beispielsweise diesen Thread auf Math Overflow (und die dort verlinkten Texte) lesen.